이 포스팅은 Algorithm Problem Solving 시리즈 113 편 중 51 번째 글 입니다.
목차
골드4 : 그래프 문제이다.
생각
이분 그래프란 무엇인가? 문제를 읽고는 파악하는 게 힘들었다. 차라리 그림으로 보는 것이 좋다.
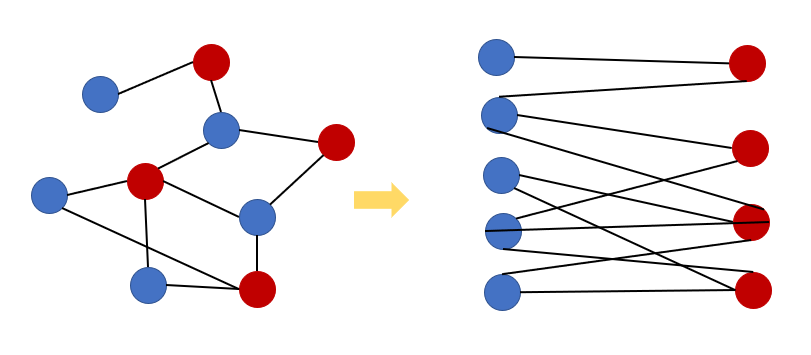
왼쪽과 같은 그래프가 있을 이걸 오른쪽 그림처럼 바꿀 수 있느냐의 문제이다. 즉 저는 두 개의 집합으로 나눴을 때, 그 집합 내에 소속되는 정점과 인접하지 않는 (서로소 관계를 유지하는) 그래프 라 할 수 있다. 여기서 핵심은 나와 인접한 노드들의 색이 반대라는 것이다.
풀이
풀이 방법은 생각 보다 간단하다. 물론 처음에는 좀 삽질을 했지만.. 여전히 그래프 문제이기 때문에 탐색 방법론 부터 생각하는 것이 합리적이다.
가장 생각하기 어려운 모양 부터 생각해 보겠다. 아래의 예는 그래프가 발생했을 때, 닫힌 그래프로 구성이 되어 정확하게 3개로 쪼개지는 경우에 대해 생각해 본 것이다.
- 닫힌 그래프는 여러개 존재할 수 있다. (그래프 입력 : a, b, c의 닫힌 그래프로 나뉜다고 가정해보자.)
- 각각의 닫힌 그래프에서 이분 그래프가 되기 위해서는 나와 인접한 노드의 색이 반대여야 한다. (a 그래프에서 이분 그래프인지 확인한다.)
- 이렇게 모든 닫힌 그래프에서 이분 그래프인지 확인했을 때 하나라도 이분 그래프가 아니라면 “No”를 출력한다.
- 모든 닫힌 그래프에서 이분 그래프라면, 이 세 닫힌 그래프를 합쳐도 이분 그래프이기 때문에 “YES”를 출력한다.
이번에는 4개의 node에서 2개의 노드만 연결되었을 경우를 생각해 보자. 연결이 되지 않은 노드는 색을 어떻게 칠해주냐에 따라 다르므로, 결국 연결된 그래프에 대해서는 이분 그래프인지를 확인해 주면 된다.
Code
#include<iostream>
#include<vector>
#include<string>
#include<cstring>
#include<iomanip>
#include<cmath>
#include<algorithm>
#include<queue>
#define MAX 20000
#define RED 1
#define BLUE 2
using namespace std;
vector<int> graph[MAX+1];
int isVisited[MAX+1];
int V, E;
// 내 노드에서 부터 시작해서 연결된 친구들을 다른 색으로 바꾼다.
// 이미 색이 칠해져 있으면 탐색하지 않는다.
void dfs(int voltex, int color){
isVisited[voltex] = color;
for (int i = 0; i < graph[voltex].size(); i++) {
int nextVoltex = graph[voltex][i];
if (!isVisited[nextVoltex]) dfs(nextVoltex, 3-color);
}
}
// 나랑 연결된 친구들은 다른 색이어야 한다.
bool isBipartiteGraph(){
for (int i = 1; i <= V; i++) {
for (int j = 0; j < graph[i].size(); j++) {
int nextVoltex = graph[i][j];
if (isVisited[i] == isVisited[nextVoltex]) return false;
}
}
return true;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int T;
cin >> T;
for (int tc = 0; tc < T; tc++) {
cin >> V >> E;
for (int i = 0; i <= V; i++) graph[i].clear();
memset(isVisited, 0, sizeof(isVisited));
for (int i = 0; i < E; i++) {
int v1, v2;
cin >> v1 >> v2;
graph[v1].push_back(v2);
graph[v2].push_back(v1);
}
for (int i = 1; i <= V; i++) {
if (!isVisited[i]) dfs(i, RED); // 색을 배정 받지 않은 친구들 탐색
}
if (isBipartiteGraph()) cout << "YES" << '\n';
else cout << "NO" << '\n';
}
return 0;
}