이 포스팅은 가볍게 이해하는 컴퓨터 시리즈 7 편 중 3 번째 글 입니다.
목차
CPU의 동작방법을 알아보자.
최호성님의 유튜브 강의를 보며 기본적인 컴퓨터 구조를 이해하고 정리하자.
디지털 회로
기본적으로 연산을 수행하도록 가능하게 하는 것은 이 디지털 회로가 있기 때문이다. 이 디지털 회로는 반도체의 특징을 이용하면 가능하다. 반도체는 조건에 따라 도체가 될 수도, 부도체가 될 수도 있다. 이 성격을 이용하여 우리는 연산을 가능하게 만들 수 있다.
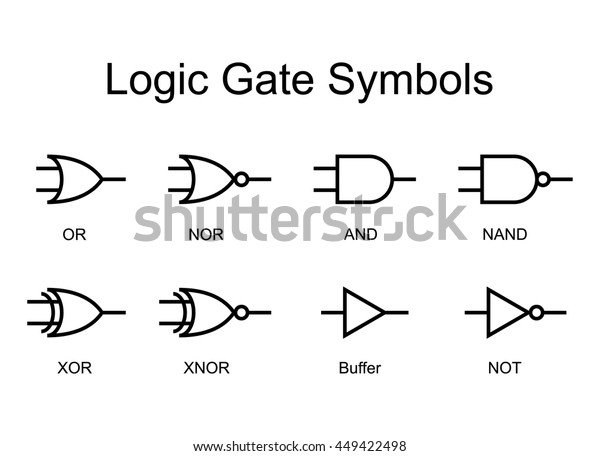출처 : https://www.shutterstock.com
연산 방법
CPU의 핵심 기능인 연산은 어떻게 구현할까?
가산기
2진수를 더하는 방법에 대한 방법이다.
기본적으로 우리가 덧셈을 한다고 생각해보자. 그렇다면 우리가 덧셈을 하기 위해서 필요한 파라미터는 3개이다. 각 자리에 표현되는 a, b, 그리고 그 두 수를 더했을 때 자리올림이 발생하는지를 판단해줄 c이다.
\[\;\;\;\;\;\;1\\ \;\;\;\;0010 \\ +0011\\ \;\;\;\;0101\]
3개의 input의 결과로 자리올림을 나타내는 변수, 더한 뒤 값을 나타내는 변수 이렇게 두개의 값을 뽑아낸다. 위의 4자리 2진수의 덧셈을 수행하기 위해서는 전가산기 4개가 필요하며, 각 연산을 수행한 결과는 다음 자리수의 input으로 들어가게 된다. $C_0$는 0이다.
뺄셈은..?
컴퓨터는 덧셈으로 끝난다.
뺄셈은 보수의 덧셈 후 자리버림을 통해 구현이 가능하다.
일반 뺄셈
\[3 - 2 = 1\]보수 덧셈 후 자리버림
\[3 + 8 = 11 => 1\]2진수에서 보수는 $0^c = 1$, $1^c=0$ 이다. 그런데 신기하게도 이 보수는 NOT연산으로 구현이 가능하다.
보수란
보수는 해당 숫자를 진법의 숫자에서 뺀 것을 말한다. 예를 들어 2의 보수는 $10-2=8$이다.
곱셈은..?
곱셈은 더하기의 연속적인 과정이다.
계속해서 더하면 곱셈구현이 가능하다. 혹은 비트 연산 중 왼쪽 shift를 사용하면 가능하다.
나눗셈은?
\[10 /3 = 3 \\\] \[10 -3 = 7 \\ 7-3 = 4\\ 4-3 = 1\\\]나눗셈은 뺄셈의 연속적 과정에서 나오는 결과이다.
세번 수행했고, 뺄셈이 불가능할 경우에 정지하면 몫과 나머지를 구할 수 있다.
혹은 오른쪽 shifting을 하면 가능하다.
0으로 나누기
이런 방법이기 때문에 0으로 나누는 경우 무한루프에 진입할 수 밖에 없다. 따라서 CPU가 과열되서 터진다…. 펑!
결론
CPU는 연산이 핵심이다. 그리고 그 연산은 더하기만으로 구현이 가능하다.